Title: Quantum Simulation of Many-body Systems Using Arrays of Individual Rydberg Atoms.
When: Wednesday, October 2, (2019), 12:00.
Place: Department of Theoretical Condensed Matter Physics, Faculty of Sciences, Module 5, Seminar Room (5th Floor).
Speaker: Daniel Barredo, Laboratoire Charles Fabry, Institut d’Optique, CNRS Palaiseau, France.
Quantum spin Hamiltonians can describe a large variety of condensed matter systems such as quantum magnets, topological insulators, or high-temperature superconductors. During the last decade several platforms, including cold atoms/ions, superconducting circuits or polar molecules, have been explored to simulate those models that are otherwise difficult to study using classical methods, even for a few tens of particles.
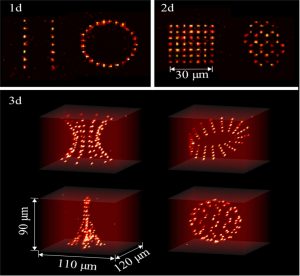
This talk will present our progress towards quantum simulation using arrays of individual Rydberg atoms [1]. We use holographic methods and atom-by-atom assembling to generate defect-free arrays of up to 70 atoms, with almost full control of the geometry in one, two, and three dimensions [2,3]. Laser excitation of the atoms to Rydberg states provides the strong, tuneable interactions needed to engineer different types of spin Hamiltonians. Using van der Waals interactions, we implement the Ising model in several geometries and measure the coherent evolution of the system after quantum quenches, or slow ramps of the experimental parameters. We observe the build-up of correlations in lattices and the onset of antiferromagnetic ordering [4,5]. Using resonant dipole-dipole interactions, we implement the XY Hamiltonian and study new topological phases of matter, as illustrated by our recent observation of a symmetry protected topological phase of interacting bosons in one dimension [6].
References
A. Browaeys, D. Barredo, and T. Lahaye, J. Phys. B 49, 152001 (2016).[2] D. Barredo et al., Science 354, 1021 (2016).
D. Barredo et al., Nature 561, 79 (2018).
H. Labuhn et al., Nature 534, 667 (2016).
V. Lienhard et al., Phys. Rev. X 8, 021070 (2018).
S. de Léséleuc et al., Science 365, 775 (2019).